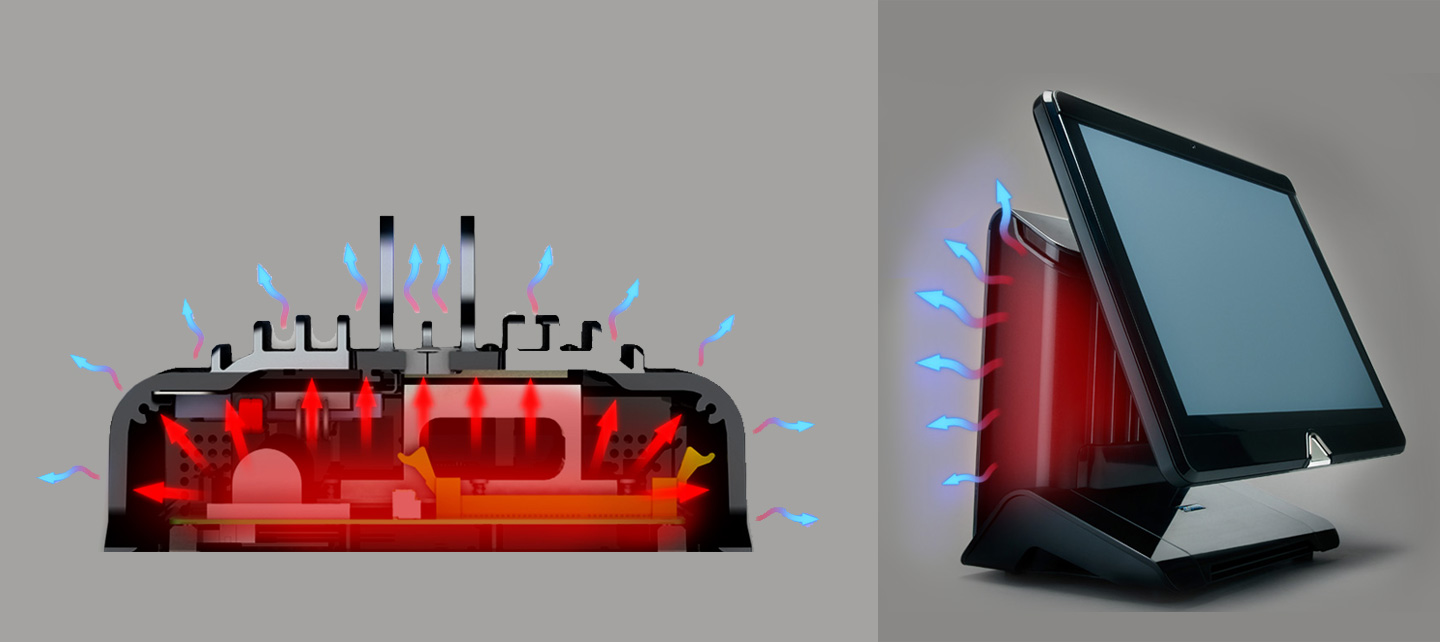
When people think of mathematics they don’t immediately associate the discipline with product design.

Advances in science and engineering have a clear link with the products available on today’s marketplace. For example, new materials and composites have allowed the creation of more energy efficient designs in the aviation and automotive industries. However, the process of developing an equation, such as the famous E=mc^2 from Einstein’s theory of special relativity, can also benefit the design process. In this article, i4pd’s Systems Analyst, Reg Harsley, will explore the value of mathematical modelling as an essential pillar of good product design.

What is a mathematical model?

In short, a mathematical model is a group of equations that can be used to describe how something behaves in a certain environment. Typically we associate this with physics and engineering problems, such as examining forces on bridges, or what comes out from a high speed collision of sub-atomic particles. However, mathematical models can be applied to a wide range of fields including finance (calculating how much a stock is worth), biology (working out how decreasing food supplies can affect a species population), and politics (predicting who will win a general election). In all of these cases, information about the system is used to create a set of predictions, and the predicting element is what can help with product design.

Prosthetic design

The role of a prosthetic limb is to return as much functional use as possible to the user. A “straightforward” design approach would be to directly copy the part of the anatomy that has been lost. However, even if we ignore the fact that human-robot interfaces are still not at a level to fully control an artificial limb, such a design, due to the large number of “parts” in a limb, would be incredibly expensive and inaccessible to a large part of the global population.

Instead of copying the lower limb anatomy, Amos Winter et al. looked at what kind of design would recreate a normal walking gait. As shown in the below diagrams, even relatively simple methods of recreating the movement in an ankle and foot can result in a large number of parts (and associated manufacturing costs).

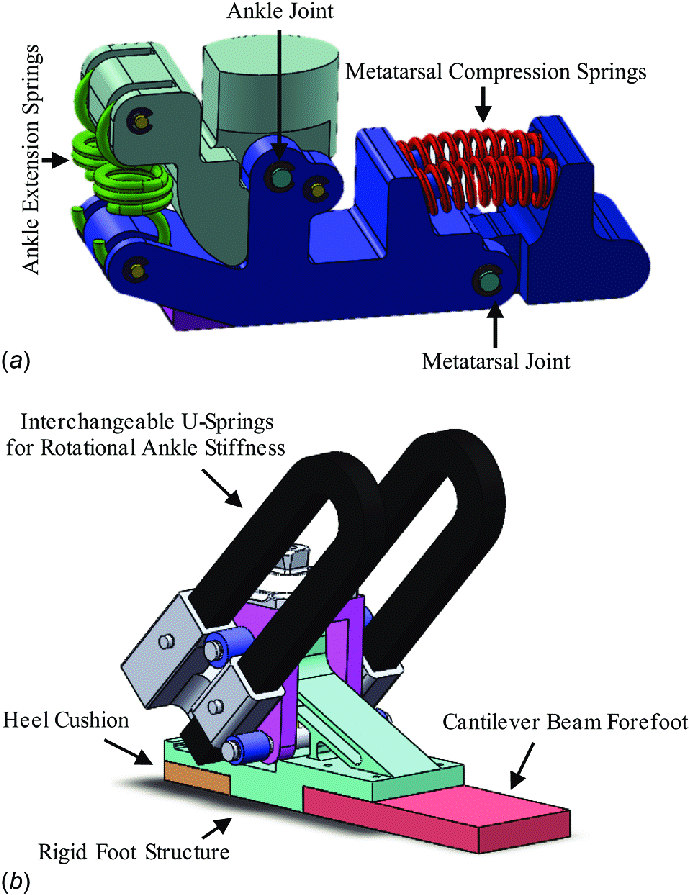
To keep costs down, the team investigated a design that could be manufactured as one part: a simple mathematical curve that could be significantly changed with only a handful of parameters. They then modelled the external and internal forces that would act on the prosthetic foot when being used for walking. By analysing these forces over a single step Winter et al. could see how the prosthetic flexed, which allowed them to predict the position of the user’s knee. These results were then compared with measurements taken from a non-amputee walking. Rather than manufacturing multiple variations of the design, the researchers worked through all of the designs in simulations.  Along with reducing the costs in the design process (the designs didn’t need to be manufactured to be tested), the simulations also allow for tailoring the design to the individual’s body: the user’s weight and leg length can be put into the simulation to determine the best foot design for them.

When such a functional form is produced through mathematics the look of the resulting product can be haphazard/unappealing. Indeed the end result of the study produced a shape that, in appearance, was more akin to a doorstop than a foot, but the design was extremely effective at copying the gait of a non-amputee.

This is where industrial designers are key to styling/embellishing around the functional elements to offer a more desirable look and feel for the end user and comfortable interface to the limb.

In our own projects, this approach to development where mathematical modelling going hand-in-hand with industrial design has led to superior performance and feedback form the users.

Acoustic voxel

The Acoustic Voxel system works by connecting small cavities together within a larger structure. The air in each of these voxels vibrates at a particular frequency, dependent on each of the cavity’s physical dimensions, and a complex resonating pattern can be created by connecting several voxels together. The resonance of the voxel system can be used to change sound played into the structure through a phone, or to create new musical instruments (anyone fancy taking up the musical hippo?). As the voxel system is contained within a structure, an audio fingerprint can be created that stores information about the object, adding a unique identifier to a product.

Now, why is mathematical modelling important for this application? As in the case of the prosthetic foot example above, modelling can be used to reduce development time. Rather than manufacturing multiple voxel systems and measuring their resonance behaviour, a designer can select the frequencies they want the voxel system to resonate at. Working back from these requirements, a mathematical model can then select the correct voxel dimensions and connections to produce these resonances.

What i4pd can do for you?

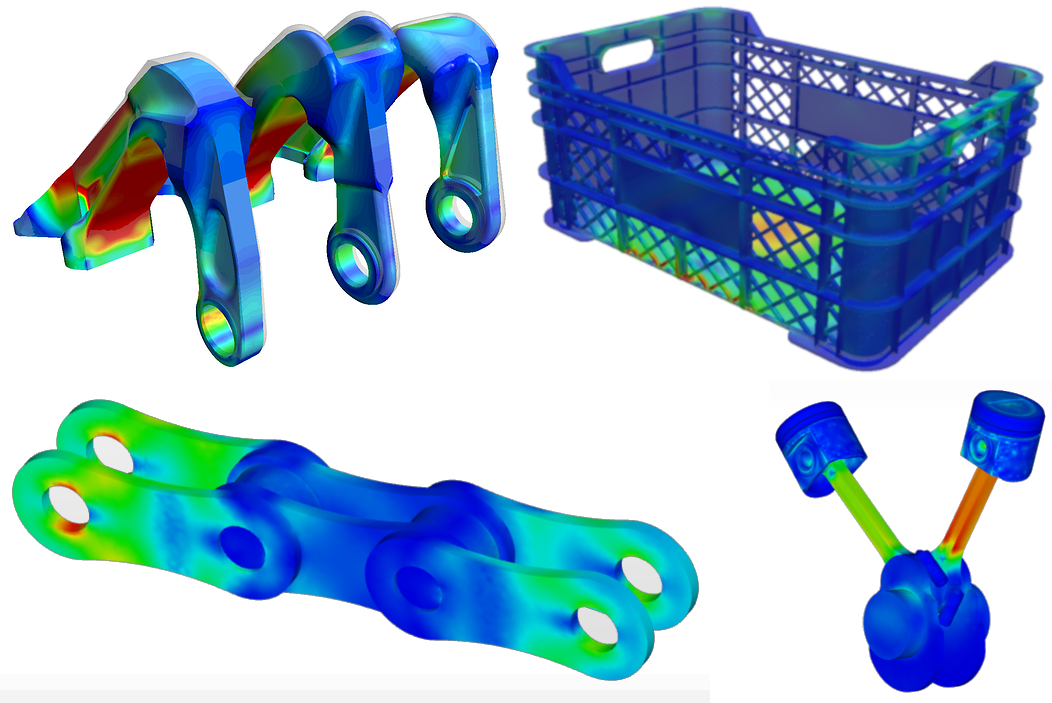
At i4 Product Design, we’ve been making use of mathematical modelling tools in our design process. For example, we implement finite-element modelling in CAD simulations as a procedure to analyse the stress applied to components that make up a product. This helps refine a design before producing expensive tools for parts. We also use mathematical modelling for more complex scenarios, where simulation packages are yet to be developed, such as dynamic heat transfer between components of a complex systems.

Do you have a complex process that requires parameter refinement? Do you know some of the mathematics that is involved in your problem, but not sure how to solve it? Why not get in touch and see what i4pd can model up for you.